
Vocabulary
• Depth: How deep the rille is.
• Distance: How far from the edge of the rille to its center.
• Rille: A collapsed lava tube that resembles a small canyon.
• Rope Length: The amount of rope needed to descend Hadley Rille.
• Rope Weight: The mass of the rope per standard length.
• Slope: The angle the rille wall makes to the horizontal.
Narrative
Apollo 15 landed near Hadley Rille in the Apennine Mountains of the Moon back in 1971. It has been heralded as the most scientifically robust of all the Apollo expeditions. Its Commander, Dave Scott, and Lunar Module Pilot, Jim Irwin, were indeed true explorers. They had even wanted to take a sample of rocks from the bottom of the rille. The idea was to tie a rope to Scott with Irwin acting as an anchor. Scott would shimmy down the slope of the rille while Irwin would play out the line. It was considered a dangerous plan with a high scientific return.
It was not approved.
But what if NASA had said yes? How much rope would Scott have needed? How much would the rope have weighed? And what was the slope of the rille that the Commander would have had to traverse?
Analysis
NASA studied the Moon prodigiously before going there, and took great pains to select each precious landing site. Thus, Hadley Rille was fairly well known geographically.
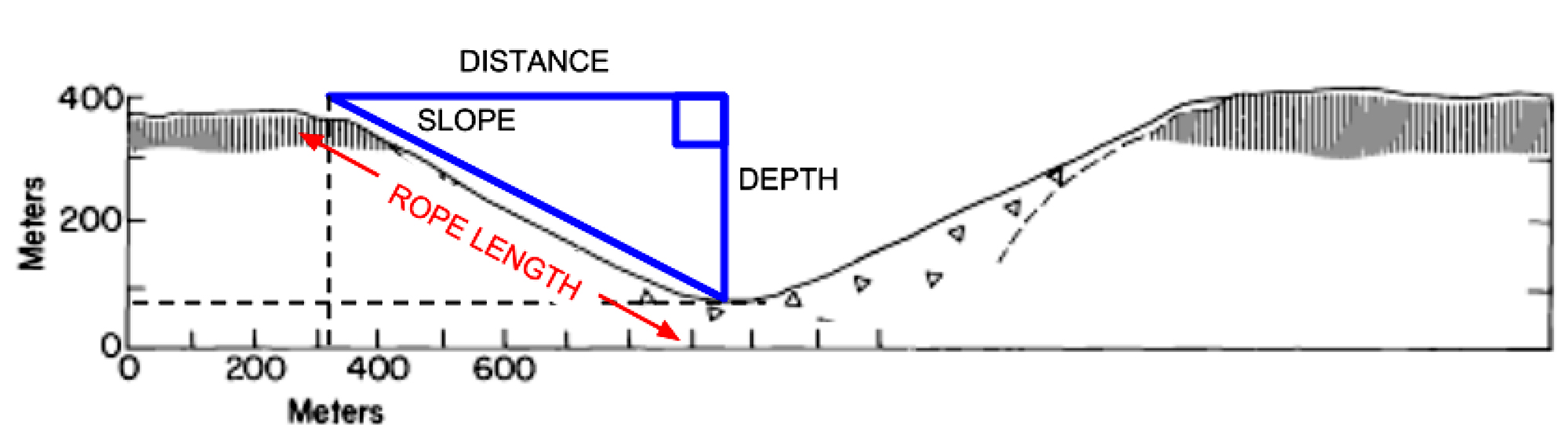
To solve this hypothetical problem, we use basic trigonometry. The hypotenuse of the triangle is the length of rope needed for the traverse, the adjacent side is the Distance, and the opposite side is the Depth. The slope is the angle between the hypotenuse and the adjacent side. Dashed lines are provided to help with the measurements.
© Lunar and Planetary Institute • Provided by the NASA Astrophysics Data System
The length of the rope can be found using the Pythagorean Theorem:
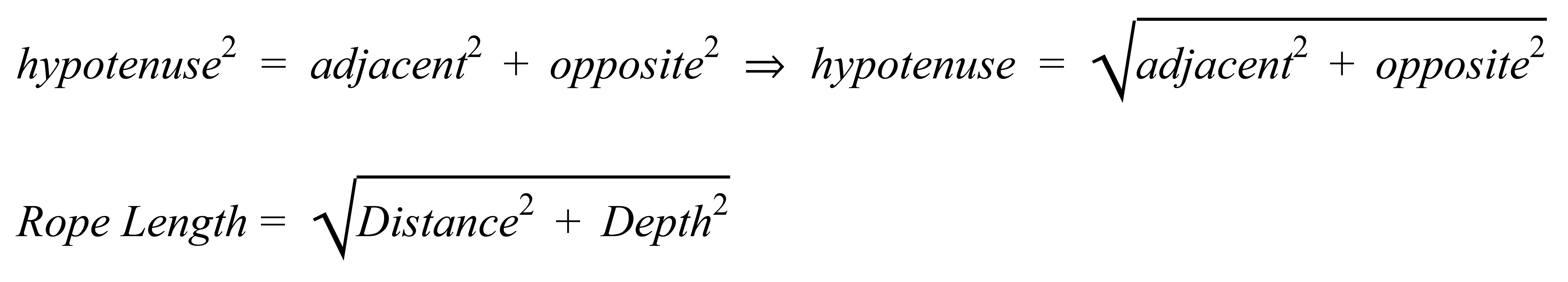
A one-half-inch diameter nylon rope weighs in at 100 grams per meter, or 0.1 kg/m. Therefore,
![]()
The Slope can be found using one of the trigonometric identities. Since we are given the opposite (Depth) and the adjacent (Distance) sides, we can use the tangent ratio.
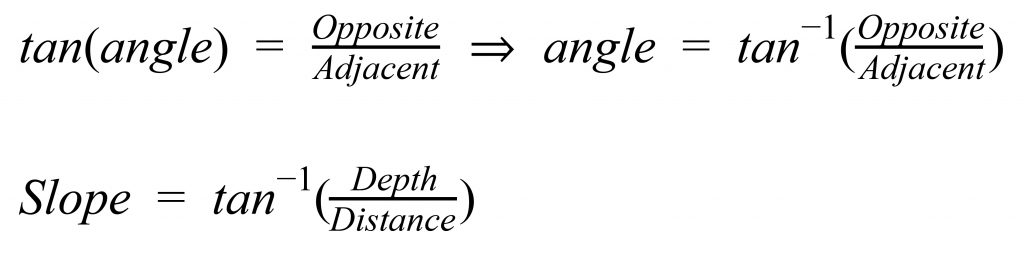
We’re assuming that a gradient of anything less than 45º is within acceptable limits.
Example
In an alternate universe, NASA decided to go ahead with the endeavour into the maw of Hadley. How much rope was needed for this wild and crazy idea, how much was the weight of said rope, and what was the slope of the rille that the Commander would have negotiated?
From the NASA image, the Distance and Depth can be determined.
Distance = 950 – 320 = 630 m
Depth = 380 – 80 = 300 m
Therefore, the length of rope needed is

The weight of the rope is

In other words, the rope is almost 2,300 feet long and weighs over 150 pounds!
The slope of the rille face is
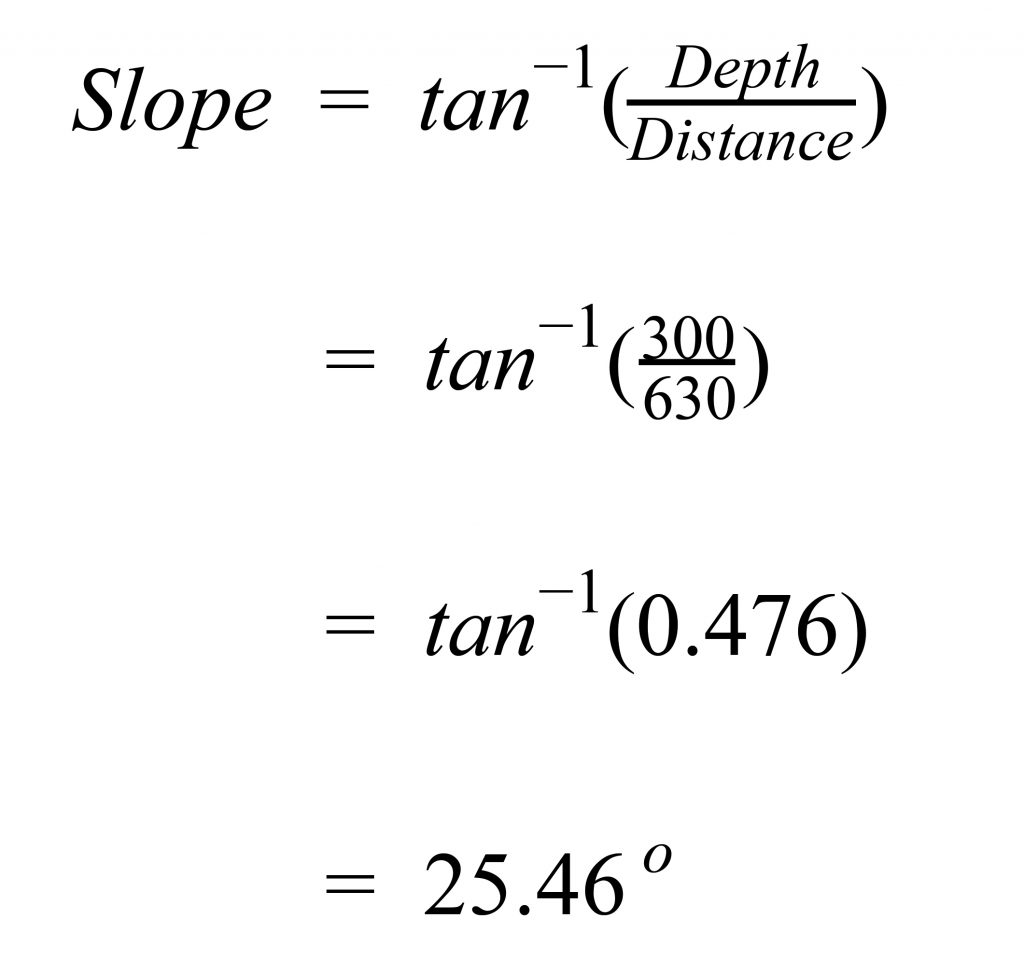
Conclusion
The slope being way less than 45º implies that there would not have been too much of a problem traversing it, especially in a one–sixth Earth gravity environment. However, even though the trip to the bottom and back was technically feasible and scientifically desirable, we’re not quite sure it would have been worth the 70 kilograms (yikes!) of rope needed to complete the journey.
Maybe NASA made the right call after all?
For a more in-depth treatment of this high school project by Joe Maness & Rich Holtzin visit www.stemfortheclassroom.com.



