
Vocabulary
• Altitude: The distance a spacecraft is above a given point on the ground
• Distance From Spaceport: The ground distance from the edge of the runway to the spacecraft
• Glide Distance: The distance the Landing Laser measures to the spacecraft
• Glide Slope (Ø): The angle a spacecraft makes to the horizontal
• Landing Laser: The laser used to determine the line-of-sight distance to a spacecraft
Narrative
Most spacecraft returning from space are always out of propellant. This is because all of the propellant is used up during the trip into space; consequently, there is none available for the trip back.
Wait. What? So how does it land?
All machines that have wings can glide, that is, fly with the engine(s) turned off. Some glide better than others, but still, they all glide.
The key to gliding in an unpowered spacecraft is speed. The faster the spacecraft flies through the atmosphere, the more efficient the wings. Thus a more efficient glide. Altitude is the other important component, in that altitude allows the spacecraft to build up speed if needed. This is why spacecraft come in with their nose down; they are maintaining their airspeed. As they cross over the edge of the runway, the nose is pulled up and the spacecraft flattens out its glide as air is packed underneath the wings. It’s then just a simple matter of letting the spacecraft sink to a gentle touchdown. Once on the ground the nose is kept in the air “wheelie” fashion, so that speed can be bled off without using brakes because they can get very hot very quickly. After the nose comes down on its own, the brakes can then be (sparingly) applied. Eventually, the spacecraft rolls to a full stop. Back home once again!
Analysis
So, at any point in the glide, what was the Altitude and the Distance from the Spaceport of the spacecraft that just landed? Good question! Why, just the other day some high school students at The Learning Community Charter School (www.tlcnm.net) were asking the same question.
We need two pieces of information to get started: the Glide Distance (GD) and the Glide Slope (Ø). We will use the Landing Laser to determine this distance and the angle. It will take a “snapshot” of this information whenever we need.
Once we have Glide Distance and Glide Slope, which is to say, once we have a side and an angle, we can form a Right Triangle.
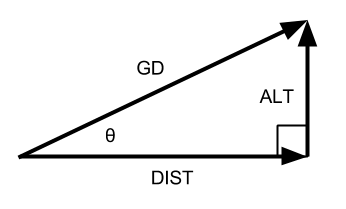
Therefore, we can use trigonometric identities to solve for the other two sides. We also see that the Glide Distance becomes the hypotenuse of the right triangle. Moreover, since cosine is defined as the adjacent side divided by the hypotenuse, and sine is defined as the opposite side divided by the hypotenuse, we can write the two trigonometric equations using this information.
cosØ = DIST / GD
sinØ = ALT / GD
Solving for Distance and Altitude, we get
DIST = GD * cosØ
ALT = GD * sinØ
We can now calculate the altitude and the distance to the Spaceport for our spacecraft.
Note: we will be using degrees instead of radians to keep things a little simpler. We will, of course, always continue to convert to S.I. units.
Example
The Landing Laser at this moment in time reads a Glide Slope of 35 degrees with the spacecraft at 15 miles distant. What is the altitude and ground distance from the Spaceport of the returning spacecraft?
We must first convert 15 miles to meters, which comes to about 24,140 m. Therefore,
ALT = 24140 * sin(35) = 13,846 m
DIST = 24140 * cos(35) = 19,774 m
Conclusion
When the spacecraft is about 15 miles distant, it is at an altitude of 13,846 m (8.6 mi) above the ground, and is 19,774 m (12.3 mi) from Spaceport America.
Is there a way that we can make a quick check of our results? Sure there is! Use the Pythagorean Theorem. Leaving the units in miles, we get:
a2 + b2 = c2
(8.6)2 + (12.3)2 ?= (15)2 = 225
(73.96) + (151.29) = 225.25
The result is close enough to 15 squared. We therefore are on track to a safe landing!
S.T.E.M. education…Don’t come home without it.
For a more in-depth treatment of this high school project by Joe Maness & Rich Holtzin visit www.stemfortheclassroom.com.



