Fly me to the Moon (on the Boeing Space Tug)

Vocabulary

Crew Module (CM): The part of the spacecraft where the astronauts live and work

Crew Module Weight: The total weight of the CM including provisions and the crew

Crew Size (Crew): The total number of astronauts needed to conduct a specific space mission

Dry Weight (m₁): The weight of the spacecraft fully loaded excluding the propellant

Engine Module (EM): The part of a spacecraft that holds the propellant tanks and the rocket engine

Exhaust Velocity (v_EXH): The speed of the escaping gas exiting a rocket engine

Gross Weight (m₀): The weight of the spacecraft fully loaded including the propellant

Inert Weight: The empty weight of the EM

Lunar Orbit Insertion (LOI): The rocket burn that places a spacecraft into Low Lunar Orbit (LLO)

Mid-Course Correction (MCC): The rocket burn that keeps the spacecraft on course

Mission Duration: The total time needed to accomplish a specific space mission

RL10 Engine: The name of the rocket engine used in the Engine Module (EM)

Standard Gravity (g₀): The acceleration due to free fall on Earth, equal to 9.80665 m/s²

Specific Impulse (I_SP): The force with respect to the amount of propellant used per unit of time

Trans-Lunar Injection (TLI): The rocket burn that places a spacecraft on a trajectory to the Moon

Narrative

A long time ago, in a galaxy very near our own, there once existed a wondrous vision of the future, where spacecraft were bountiful, and imaginations could soar.

Given our astronautics concepts for S.T.E.M. education projects, the Boeing Space Tug Study (circa 1971) exemplifies this penultimate vision. Notably, it was a complete design that not only included a Crew Module (CM), but also an Engine Module (EM).

The CM would have housed the astronauts and all of their supplies, including food, oxygen, science equipment, etc.

The EM would have contained the rocket engine, propellant, tanks, electrical supply, etc.

The CM and EM were to be attached together, and the two would have become one, as they say. The design was very much similar to the Apollo spacecraft that heralded NASA’s endeavors in the so-called space race of that era. Hence, a near twin to the Apollo design.

It really would have been quite an awesome machine, because the EM could have been able to carry any type of payload, whether it was the CM or satellites or whatever. Overall, the Boeing Space Tug design was inspirational as well as functional. Remarkable for the year 1971!

That being said, the spacecraft was never built! However, we can still make something good out of its advanced design. Namely, our S.T.E.M. classroom projects geared to this study posits our students working on real space missions using a real spaceship model and real numbers. In short, there are real-world implications in our applied concepts and mathematics.

So can we make this space vehicle finally fly in space; all the way to the Moon? You bet your last rocket!

Analysis: CM

Spacecraft habitat weight depends on many factors, such as the number of astronauts needed or the duration of the mission. Some CM component weights will vary depending on these factors (such as Environmental Control and Life Support Systems), while others will weigh the same no matter what (such as the CM structure itself).

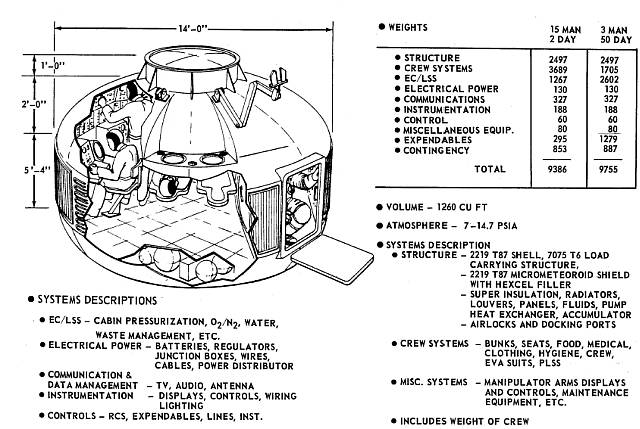
The Space Tug CM graphic shows that a crew of fifteen would have allowed for a two-day mission, and the CM would have weighed 9,386 pounds, whereas a crew of three would have yielded a fifty-day mission and would have weighed 9,755 pounds (all figures would have included the weight of the crew). These numbers look suspiciously like points on a Cartesian graph, which means that they may be linear equations.

We’ll make the Crew Size (Crew) the independent variable. Therefore we get the points (3, 50) & (15, 2) and (3, 9755) & (15, 9386). We can thus calculate the slope and the y-intercepts of the two linear equations.

Slope₁ = 2 – 50 / 15 – 2 = -48/12 = –4

y–int₁ = 2–(–4)(15) = 2 + 60 = 62

Slope₂ = 9386 – 9755 / 15 – 3= –369 / 12 = – 30.75

y – int₂ = 9386 – (– 30.75)(15) = 9386 + 461.25 = 9, 847.25

Therefore, the two linear equations for the Boeing Space Tug CM are:

Mission Duration = 4Crew + 62

Weight_CM = –0.75Crew + 9847.25

Example

Suppose you want to take a crew of 10 astronauts on a space mission to the Moon. What would be the Mission Duration of the spaceflight? More importantly, what is the weight of the CM?

Using the linear equations that we just derived, we plug in Crew = 10 into the equations.

Mission Duration = – 4(10) + 62 = 22 Days

Weight_CM = – 30.75(10) + 9847.25 = 9, 540 lbs

So for this particular design, a crew of ten would have allowed the spacecraft to stay aloft for about three weeks, and would have weighed under 10,000 pounds. Very nice!

Analysis: EM

The CM wouldn’t have gone anywhere unless there was a way to make it go. Enter the Engine Module (EM). This machine would have had everything you needed to go on a space mission: propellant tanks, a Reaction Control System (RCS), batteries, and of course, the reliable RL10 rocket engine. This rocket engine was useful in that it could have been restarted many times, burning the highly efficient Liquid Hydrogen (LH₂) fuel. This meant that the EM could have been reused many times, reducing the cost of flying in space!

Speaking of flying in space, the most useful equation in all of rocketry is appropriately called the Rocket Equation, also known as the “Tsiolkovsky Equation” named after its discoverer.

∆v = v_EXH · ln(m₀ / m₁)

It tells rocketeers how much of a change in velocity (∆v) is available given the payload weight, the propellant weight, and the exhaust velocity (v_EXH) of the gasses being expelled by the rocket. The exhaust velocity of a rocket is the engine’s Specific Impulse (I_SP) multiplied by the standard gravity of Earth.

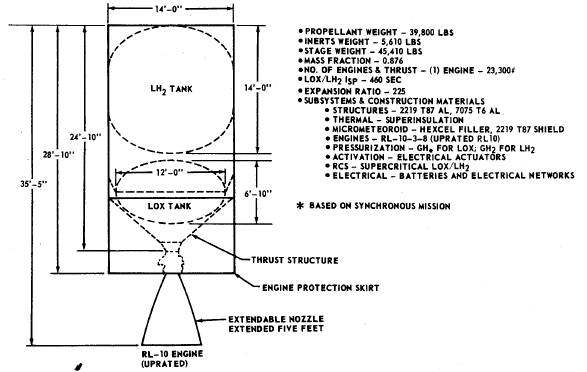
Using the information from the Space Tug EM image, we see that the RL10 (with the rocket nozzle extended) had an I_SP of 460 s. We can thus calculate the rocket engine’s Exhaust Velocity (V_EXH).

v_EXH = I_SP · g₀ = (460)(9.80665) = 4, 511 mps

The EM graphic also tells us that the Inert Weight of the EM was 5,610 lbs. If we carry a CM with a crew of 10 astronauts on a 22–day mission that weighs 9,540 lbs, and we also carry, for instance, 8,000 lbs of scientific and other payload, the Dry Weight can be calculated.

m₁ = Weight_INERT + Weight_PAYLOAD + Weight_CM = 5610 + 8000 + 9540 = 23,150 lbs

Finally, the EM graphic shows that the propellant would have weighed 39,800 lbs. We now have everything we need to solve the rocket equation.

m₀ = m₁ + Weight_PROPELLANT = 23150 + 39800 = 62,950 lbs

Putting everything together, we get

∆v = (4511) · ln(62950 / 23150) = (4511) · ln(2.72) = (4511)(1.000346) = 4,513 mps

Example

The students at The Learning Community Charter School (www.tlcnm.net) have designed a mission to go one-way from a Bigelow space station in Low Earth Orbit (LEO) to a Bigelow space station in Low Lunar Orbit (LLO) (we’ll assume that the spacecraft propellant tanks will be replenished at the lunar space station for the return trip home). The spaceflight would resemble the first leg of the historic Apollo 8 lunar orbit mission. Will they make it?

Looking up the ∆v requirements for the Trans Lunar Injection (TLI), the Mid-Course Correction (MCC), and the Lunar Orbit Insertion (LOI) rocket burns, we can calculate the total ∆v Budget needed to go to the Moon and enter lunar orbit.

∆v Budget = TLI + MCC + LOI = 3205 + 19 + 881 = 4,105 mps

Conclusion

For this particular spacecraft, the ∆v capability of the spacecraft of 4,513 mps exceeds the required ∆v Budget of the lunar mission of 4,105 mps. We therefore conclude that the mission can be safely flown in this configuration all the way to the Moon, and we recommend that crew selection begin immediately!

The Boeing Space Tug Study spacecraft, had it been built, would have been a most formidable and versatile ship, well ahead of its time. They truly had an astonishing space vehicle on the drawing board back in the day, no?

So why are we not building reusable spaceships en masse again?

Note: In the next issue of RocketSTEM magazine, we will continue the human adventure by working out the mathematics for a landing on the Moon. Stay tuned!

For a more in-depth treatment of this high school project by Joe Maness & Rich Holtzin visit www.stemfortheclassroom.com.

This article appeared in the 7th issue of RocketSTEM magazine.

Download PDF    Issuu Reader    Buy Print Edition