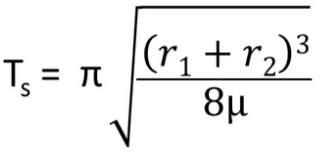How long before we get there?

Vocabulary

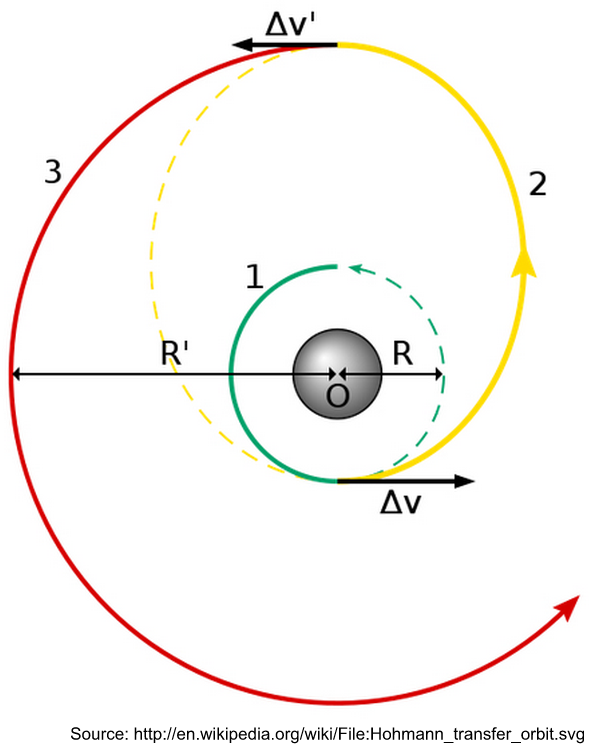
• Apoapsis Delta V Burn: The rocket firing at the highest point of a Transfer Orbit.

• Periapsis Delta V Burn: The rocket firing at the lowest point of a Transfer Orbit.

• Transfer Time: The time between apoapsis and periapsis Delta V rocket firings.

Narrative

Getting from one orbital altitude to another not only takes delta v, it also takes time. It isn’t as simple as aiming yourself and firing your rocket. Orbital mechanics is a ballet in space, where the lower your orbit the faster you go, and vise versa.

Any change in orbital velocity and you wind up in an elliptically-shaped orbit, instead of the fairly stable circular orbit.

Transferring from one orbit to another is accomplished by changing a circular orbit (represented in by the green and red circles in the image above) into an elliptical orbit (represented by the yellow curve). The Transfer Time is the time it takes for the spacecraft to follow the path of the yellow curve.

To get from one orbit to another, we must push ourselves off, and then brake when we get there. We coast in between these two maneuvers. We can calculate how much time we will coast from one point in space to another.

Analysis

The equation to calculate the transfer time from one orbital altitude to another is given by one of the Hohmann Transfer Orbit Equations:

where

• T_s is Transfer Time in seconds

• r₁ is the smaller orbital radius

• r₂ is the larger orbital radius

• µ (mu) is Earth Standard Gravity = 9.80665 m/s^2

• π (pi) is the constant 3.141592653589793238462643383279502884197169399…

The number π (pi) is involved in the equation because we are actually going around in circles.

Example

Let’s suppose you want to go from the Hubble Space Telescope (HST) to the International Space Station (ISS). How long would it take to get there?

The orbital radius is simply the sum of the orbital altitude plus the radius of the Earth. So for the HST (r1), we get 6,708.14 km, and for the ISS (r2) we get 6,948.14 km.

Plugging everything in the equation, we get 2,673 seconds of transfer time. If we divide that by sixty (seconds per minute) we get 44.55 minutes.

Conclusion

It takes about half an orbit to transfer between two orbital altitudes that are not that far apart.

This article appeared in the 4th issue of RocketSTEM magazine.

Download PDF    Issuu Reader    Buy Print Edition