Can SpaceShipTwo fly up to space?

Vocabulary

• Parabola: The graph of a quadratic equation, which for this project is in the shape of an upside-down capital “U”

• Quadratic Equation: The equation that creates a parabola when graphed

• Vertex: The maximum (or Minimum) point on a parabola

Narrative

If a baseball is thrown into the air to another ball player, it will continue moving upward after it leaves the ball player’s hand. The ball will eventually reach a maximum height (which we can calculate), and then drop back down to the other player’s glove.

Virgin Galactic’s SpaceShipTwo (SS2) follows a flight profile very similar in nature. Can we figure out how high the spacecraft went? Why, I’m glad you asked!

That baseball (spacecraft) follows a nice parabolic curve, and can be described using a quadratic equation:

h = at² + v₀t + h₀

where

• a is a constant = -4.9

• v₀ is the initial velocity

• h₀ is the initial height

Analysis

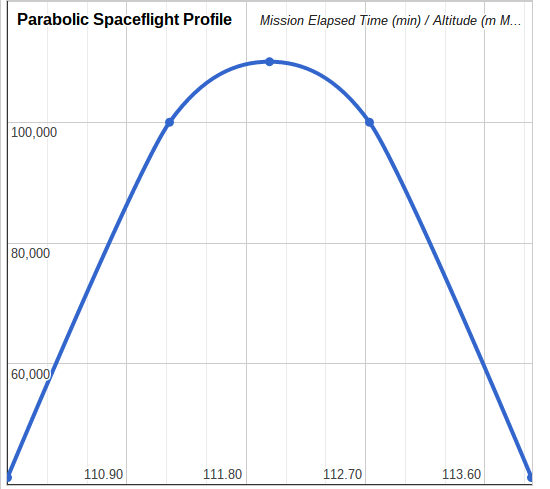
The SS2 parabolic spaceflight profile shows that the rocket engine cutoff is at a certain Mission Elapsed Time (MET) and height above Mean Sea Level (MSL). This is equivalent to the state a baseball is in at the moment a player releases it into the air.

Plugging that information into the quadratic equation allows us to calculate the time the spacecraft reached maximum altitude, and the maximum altitude itself. All we have to do is find the vertex of the parabola, since that is the point of maximum height. Once we find the time at maximum altitude, we can finally use that calculate the maximum altitude.

vertex_t = -v₀/2a

and

vertex_h = a(vertex_t)² + v₀(vertex_t) + h₀

where

• vertex_t is the time (after rocket burnout) at maximum height

• vertex_h is the maximum height

Example

Let’s suppose that the SS2 rocket burnout time is at 110 min MET at an altitude of 135,000 ft MSL with a velocity of 2,600 mph. Will it reach space, which is to say, will it go above 62 miles?

First, as always, we must convert our input into S.I. Units:

v₀ = 135,000 ft = 41,148 m

h₀ = 2,600 mph = 1,162 mps

Space = 62 mi = 100 km = 100,000 m

So,

Time of Maximum Altitude = Rocket Burnout Time + vertex_t = 111.98 min

Maximum Altitude = vertex_h = 110,027 m

Conclusion

As a result of the spacecraft breaking the 100,000 m barrier, the space tourists aboard this particular parabolic spaceflight would have all proudly earned their Astronaut Wings.

For a more in-depth treatment of this high school project by Joe Maness & Rich Holtzin visit www.stemfortheclassroom.com.

This article appeared in the 3rd issue of RocketSTEM magazine.

Download PDF    Issuu Reader    Buy Print Edition